3736. Golden sand
During robbery in a store a
thief found n boxes with golden
sand. All the sand in a box number i has
the cost vi and the weight wi. To carry the stolen sand,
thief uses a knapsack. Find the highest total cost of sand that the robber can
carry out, if knapsack capacity is limited to w.
One can pour from the boxes
any amount of sand, while the ratio of the cost of the poured sand to the cost
of the entire box is equal to the ratio of volume of the poured sand to the
volume of entire sand box.
Input. The first line contains two
integers n and w (1 ≤ n
≤ 1000, 1 ≤ w ≤ 106). Each of the next n lines contains two integers. The i-th line contains the price vi and weight wi of the sand in the i-th box. All numbers are non-negative
and do not exceed 106.
Output. Print the desired maximum
cost with 3 digits after the decimal point.
|
Sample input |
Sample output |
|
3 50 60 20 100
50 120
30 |
180.000 |
SOLUTION
greedy - knapsack
Algorithm analysis
The unit cost of
sand in the i-th box is vi / wi. Obviously, the
backpack should be loaded with as expensive sand as possible. Sort the boxes by
non-increasing cost per unit of sand (non-increasing vi / wi). Use a greedy
approach to load the knapsack.
Example
Sort the
boxes of sand in nonincreasing order of the ratio vi / wi.
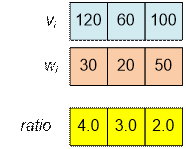
The robber can take
w = 50 sand with him. He takes with
him:
·
30 units of sand with total value 120;
·
20 units of sand with total value 60;
Thus, the total
cost of his profit will be 180.
Algorithm realization
Declare class Sand, that
contains the price of the sand price
(per unit) and the weight of the available sand weight of the cost price.
class Sand
{
public:
double price;
int
weight;
Sand(double price, int weight) : price(price), weight(weight) {}
};
The function f is a
comparator to sort the sand. The sand is sorted in descending order of its price.
int f(Sand a, Sand b)
{
return a.price > b.price;
}
Read the input
data. Store the pairs into array v: the cost of a sand unit and the weight of the sand in the
box.
scanf("%d %d", &n, &w);
for (i = 0; i < n; i++)
{
scanf("%d %d",
&vi, &wi);
v.push_back(Sand(1.0 * vi /
wi, wi));
}
Sort the boxes in non-increasing order of sand price per unit.
sort(v.begin(),
v.end(), f);
Greedily load
the knapsack. The weight of the sand that
can still be loaded into the knapsack is w. Take the i-th box. You
can put in a backpack a weight of at most min (w, the weight of the i-th box).
for (i = 0; i < v.size(); i++)
{
res += min(w, v[i].weight) * v[i].price;
w -= min(w, v[i].weight);
}
Print the cost of
sand in the knapsack.
printf("%.3lf\n", res);